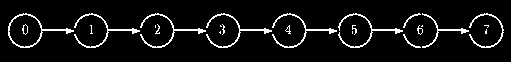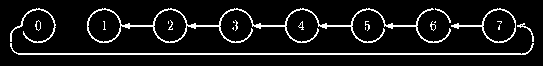Still Under Construction . . .
BLACS TOPOLOGY
The BLACS routines which operate on scopes take the parameter
TOP. This parameter determines how the messages involved in a
distributed operation are sent.
The use of the topology idea allows the user to exploit the following fact:
even if the time to perform a distributed operation cannot be reduced,
which processors bear the brunt of the cost of the operation
can be varied.
Many factors go into deciding which topology is optimal. First, the user
must decide if any processor is more important than others. For instance,
if the source processor's time is more important than other processors',
a ring topology is often optimal. On the other hand, if everyone needs
the information quickly, some type of tree is often best.
Some topologies tie up the sending processor for large amounts of time,
and different processors get the information at different times depending on
topology. Also, some topologies are "noisy", i.e. many communications
are issued simultaneously, while others are "quiet". Noisy algorithms
will cause problems on systems where network conflicts are problematic.
Quiet algorithms are likely to force some processors to wait much longer than
they would if a "noisy" topology had been used, since less communication
is going on in parallel.
Some topologies are "pipelining", i.e., the first such operation
synchronizes the processors so that subsequent operations will be cheap.
The most important choice in topologies is generally to choose whether
or not to use a pipelining topology. If the user knows he will be maintaining
a pipe for a significant amount of time, a pipelining topology (i.e. a ring
based topology) should be considered. Generally, if the user cannot maintain
a pipe, he will simply want to minimize the time for a single operation to
complete. Tree-based topologies are usually the best choice in this case.
The BLACS have a special default topology to provide for minimizing the
single operation time, and this is selected by using the default topology
TOP = ' '.
Broadcast topologies
Ring topologies and pipelining
All of the BLACS' ring topologies display pipelining to at least some degree.
When a ring broadcast is performed, it forces an obvious ordering onto
the processors; i.e, the first processor in the ring will leave the operation
before the processor which follows it in the ring. This means that once the
cost of the first broadcast is payed, the processors are optimally ordered
to perform another ring broadcast. The time each processor pays for the
second broadcast will be roughly the same as for a single point to point send.
Therefore, whenever a given processor is to issue several
consecutive broadcasts, use of a ring topology should be considered. It
will result in minimization of the sender's time as usual, but since the
ordering cost is payed only once, it may result in faster overall transfer
rates as well.
Pipelines can be maintained if the algorithm flows across processors in
an orderly way. I.e., if the sender of row broadcasts starts out as
the first process column, and then is the second, etc, an increasing
ring pipeline will be maintained. If the flow is in the opposite direction,
it may be possible to set up a decreasing ring pipeline.
Let us define Tc to be the time it takes for a message to be
sent from one processor to another. We may use this time measurement
to provide crude estimates of the time a given broadcast will require,
and the amount of pipelining to be expected.
Unidirectional Ring
Unidirectional ring topologies require the source processor to issue one broadcast, and
each processor then receives and forwards the message. The two unidirectional
ring topologies are increasing ring (TOP = 'I'), and decreasing ring,
(TOP = 'D'). These algorithms have the advantage that the originating
processor must spend only Tc time in the broadcast.
However, the last processor
in the ring will spend (Np-1) * T_c time in algorithm.
The following figures show examples of eight node increasing and decreasing ring
broadcasts. Unidirectional rings are the "quietest" algorithms possible:
only one processor is sending at a time.
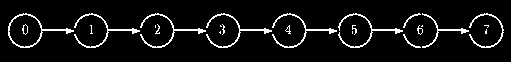
Increasing ring
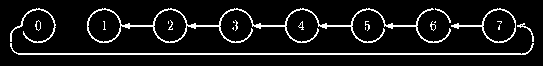
Decreasing ring
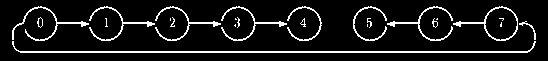
Split ring
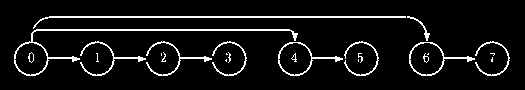
Multi-ring
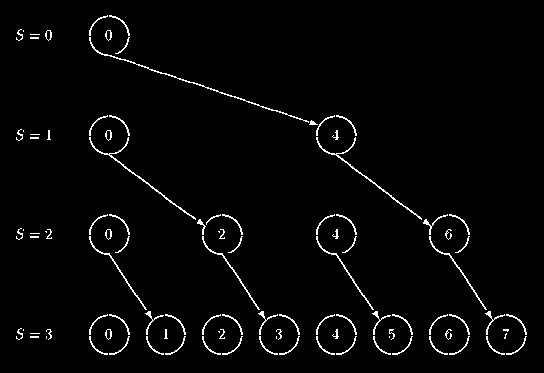
1-tree broadcast
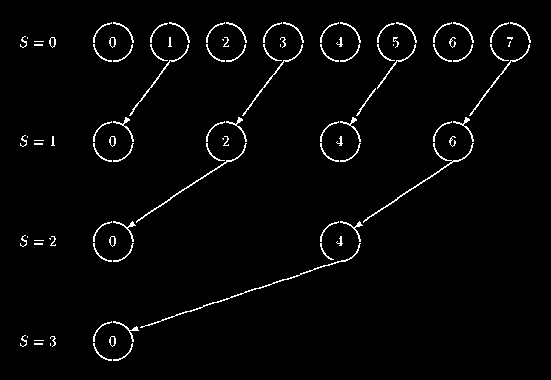
1-tree gather

Bidirectional exchange