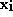Fourier Transforms

The computational of the fast Fourier transforms (FFTs) is the cornerstone of many supercomputer applications. These include not only the predictable digital signal processing, speech recognition, image processing, and petroleum seismic analysis, but also other less obvious applications, such as in computational fluid dynamics, medical technology, multiple precision arithmetic and computational number theory. Computations worthy of a parallel computer generally fall into four categories: (1) one or a few very long 1-D FFTs; (2) many small or moderate-sized 1-D FFTs; (3) one or a few large 2-D FFTs; or (4) one or a few large 3-D FFTs. The PARKBENCH \ suite includes two FFT test kernels, one for a large 1-D FFT, and one for a large 3-D FFT.

1. 1-D FFT. In this kernel, two sequences of integers and 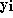are generated, with length 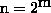and values in the range 0 <= 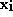, 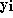< M. The standard value of M is 1024. These sequences are generated using the same uniform pseudo-random number generator as is used in the 3-D FFT kernel and the embarrassingly parallel kernel. Then the linear convolution of these two sequences is computed using a complex-number FFT, i.e. by padding x and y with zeroes to length 2n, then performing a forward FFT on x and y, multiplying the two resulting sequences of complex numbers, and finally performing an inverse FFT on the result. The result sequence should have exclusively integer values, which permits a straightforward validity check.

   No restriction is placed on the FFT technique used to perform this convolution, except that it be based on a complex-number FFT rather than, for example, a number-theoretic FFT. It is expected, however, that efficient implementations will employ techniques, such as Edson's algorithm and real-to-complex FFTs, that take advantage of the purely real nature of the input and output data to reduce the computational cost. The usage of vendor-supplied library FFT routines is permitted. The serial implementation program includes a reasonably efficient 1-D FFT suitable for computation on a workstation or single processor vector system.

2. 3-D FFT. The PARKBENCH 3-D FFT kernel is the 3-D FFT PDE benchmark from the NAS Parallel Benchmark suite [25]. It performs the essence of many spectral codes and is a rigorous test of long-distance communication performance. A brief description of this benchmark is as follows.

   Consider the partial differential equation (PDE)

   u(x,t) t &=& u(x,t)

   where x is a position in three-dimensional space. When a Fourier transform is applied to each side, this equation becomes

   v(z,t) t &=& -4 |z|^2 v (z,t)

   where v(z,t) is the Fourier transform of u(x,t). This has the solution

   v (z,t) &=& e^-4 |z|^2 t v (z,0)

   In this benchmark a 3-D complex array U, which represents u is first filled with pseudorandom data generated by the same scheme as used in the embarrassingly parallel kernel. Then we compute V, the result of a forward 3-D FFT of U. For each of several iterations, V is multiplied by the appropriate exponential factors and performs an inverse 3-D FFT on the result.

   Any complex FFT algorithm may be used for the computation of the 3-D FFTs mentioned above, and vendor-supplied library routines may be employed.